Les filtres
Les filtres sont très utile en électronique, ils permettent d’éliminer les fréquences non désirées dans les montages que ce soit en haute ou en basse fréquence. Le domaine le plus connu ou les filtres sont utilisés est le son mais ils sont également utiles dans bien d’autres domaines comme la CEM. Je vais simplement vous expliquer comment vous pouvez intuitivement savoir quel sera le comportement d’un filtre sans passer par les mathématiques (ou le moins possible).
Les différents types de filtres
Vous pouvez avec un filtre laisser passer ou couper certaines fréquences. Les Electroniciens leur ont donc donné un nom équivoque pour les nommer afin de savoir de quel type de filtre nous parlons. Nous avons donc les filtres « passe bas » qui laisse passer les basses fréquences. Les passes haut qui laisse passer les hautes fréquences. Et enfin les passes bandes et les coupes bandes qui ne laisse passez ou ne coupe qu’une bande de fréquence.
La façon de regarder un montage.
Il y a 2 façons de regarder des montages comme les filtres, la première est de les voir dans le domaine du temps. La seconde est de le voir dans le domaine des fréquences.
le domaine du temps
Dans le domaine du temps, c’est l’image que vous verrez sur un oscilloscope, c’est a dire la déformation du signal d’entré par rapport au signal de sortie. Lorsque vous mettez un condensateur comme celui ci sur un signal en forme de créneaux par exemple, vous verrez celui-ci s’arrondir. Si maintenant vous regardez le signal de sortie par rapport a celui qui est a l’entrée vous constaterez un déphasage entre l’entrée et la sortie.
Ce déphasage est appelé la phase, elle est présente chaque fois qu’il y aura un filtre sur un circuit. Le filtre produira une retard ou un avance par rapport au signal d’entré.
Le domaine des fréquences
Le domaine des fréquences est une autre façon de voir un signal électrique. Il faut imaginer que l’on applique un signal sinusoïdal a une fréquence de 1 Hz. Ensuite on augmente sa fréquence de ce signal jusqu’à 1 Mhz par exemple. Si on est en présence de simples résistances ,le signal d’entré sera toujours le même que celui de sortie et ceux a toutes les fréquences.
Si vous êtes en présence d’un filtre, vous verrez la tension de votre signal évoluer en fonction de sa fréquence.
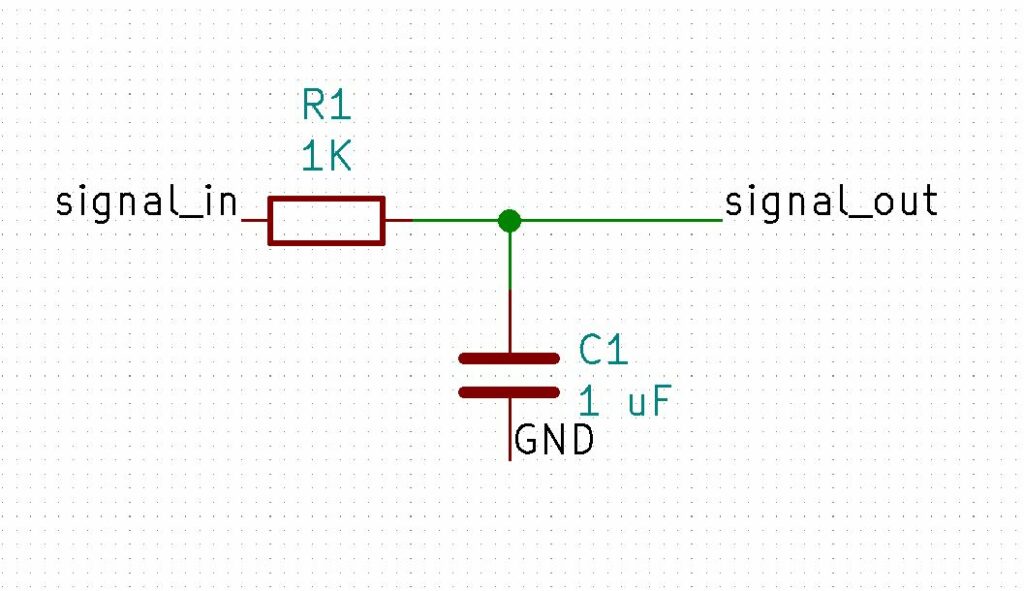
Voici un filtre passe bas
Ci-contre un filtre composé d’une résistance et d’un condensateur. Ce filtre est appelé passif car il ne nécessite pas d’alimentation pour fonctionner.
Pour comprendre comment il va se comporter en fonction du signal d’entré il faut savoir que pour un condensateur tout se passe comme si il avait une grande résistance a basse fréquence et une résistance qui tend a diminuer lorsque la fréquence augmente.
Cette résistance se calcule de la façon suivante:
1/Cω avec ω(oméga) = 2 x π x F (fréquence).
Avec les valeurs que nous avons ici ca donne:
10000 HZ -> 15 ohm
1000 HZ -> 159 ohm
100 HZ -> 1591 ohm
Comme vous le constatez la valeur de la résistance équivalente a notre condensateur diminue avec la fréquence. Il sera facile de calculer la tension a ses bornes a une fréquence donnée. Vous allez vous rendre compte qu’elle diminue avec la fréquence. Notre filtre laisse donc passer les basse fréquences et attenue les haute fréquences. Il s’agit donc bien d’un « passe bas ».
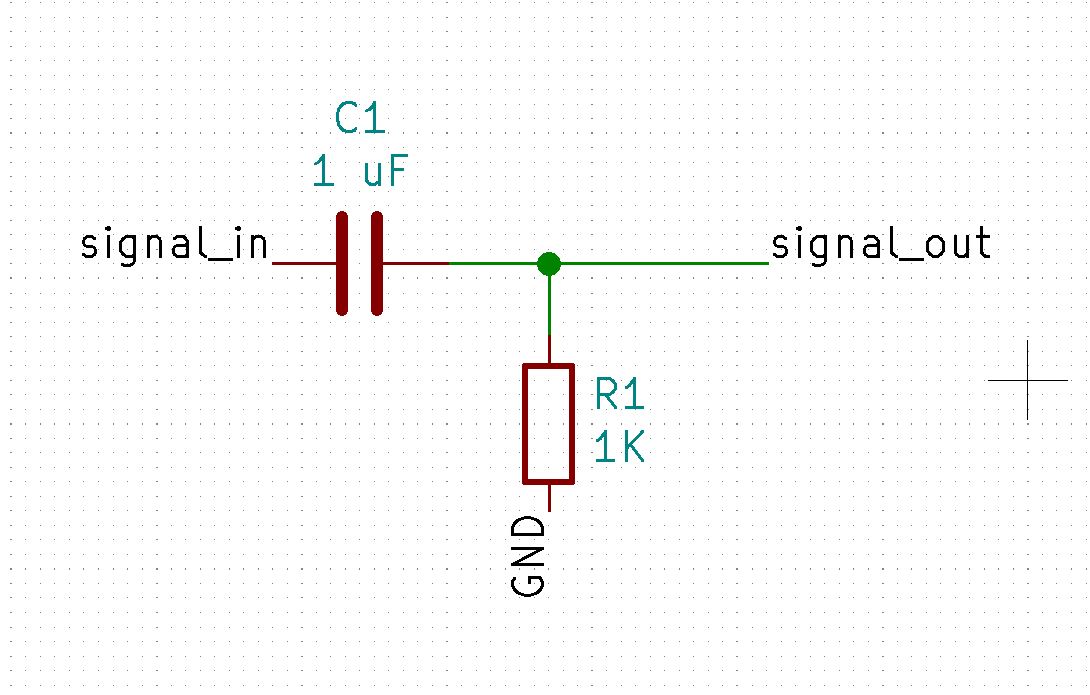
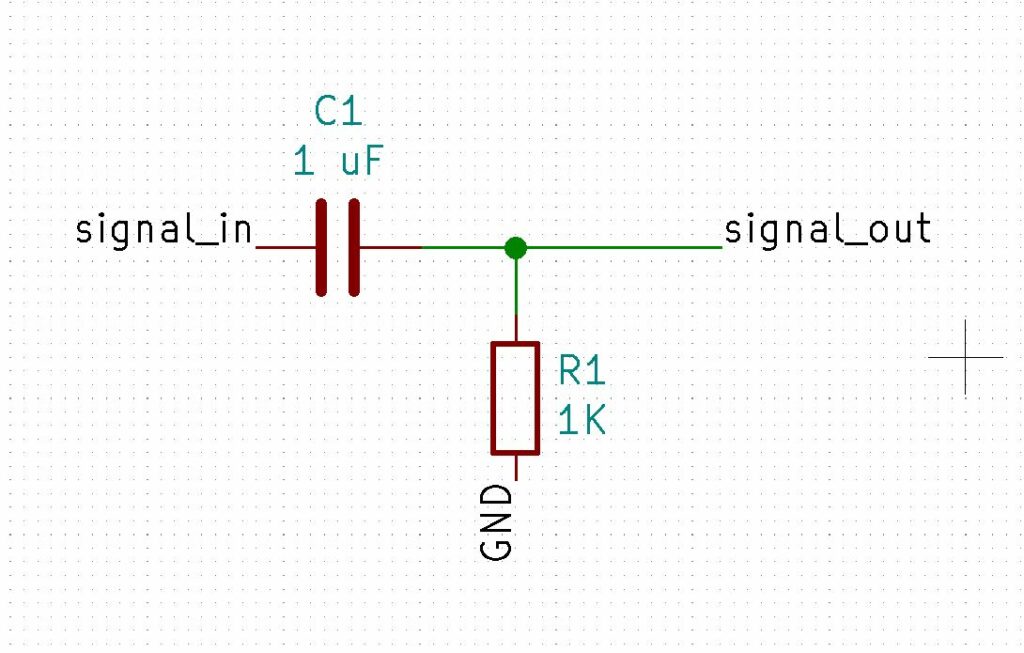
Le filtre passe haut.
Voici le même filtre mais cette fois monté dans l’autre sens. Si vous avez gardé en tète que le condensateur a une résistance qui diminue avec la fréquence, vous n’allez pas mettre longtemps a comprendre que cette fois ci plus la fréquence sera élevée plus le signal de sortie sera fort.
Il s’agit donc bien d’un « passe haut ».
J’espère que ce petit article vous aura donnée une idée de ce que sont les filtres. Sachez que vous pourrez facilement trouver plus de théorie sur ce sujet avec surtout beaucoup plus de mathématiques. Mon idée ici était de vous donner une idée assez précise de ce que font les filtres sans pour autant vous faire peur avec des mathématiques.
Merci pour votre lecture
Sylvain Altmayer